Overview

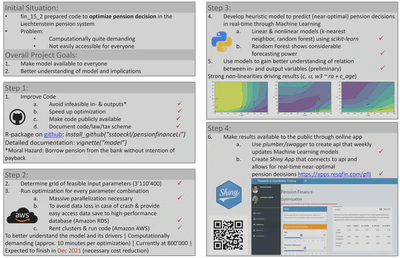
In this project we developed an R-package (available through github at https://github.com/sstoeckl/pensionfinanceLi) to optimize decisions individuals in Liechtenstein’s pension system have to take. The package contains several optimizers as well as a documentation (available through vignette("model") once the package is installed). We have started the optimization for a feasible parameter grid to determine which variables are the most relevant drivers of optimal pension decisions. Based on the results we have trained three machine learning models (a hyper-parameter-tuned random forest performs best) to allow individuals to receive faster and near-optimal decisions without having to wait for the individual optimization on each run (up to 25 minutes on a regular CPU). Predictions from these models are available to the public at https://apps.resqfin.com/pfli where - based on each persons individual settings.

Step-by-Step Project Description

1. We have built an R-package (pensionfinanceLi, can be installed in R as devtools::install_github("sstoeckl/pensionfinanceLi")). This was a necessary pre-cursor for the following optimization procedure, as we wanted to carefully double-check that no undesired/counter-intuitive results would be produced by our optimizer.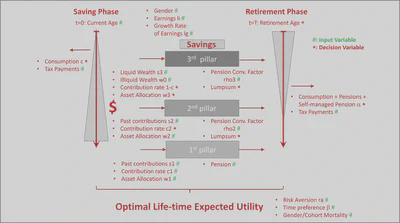

   

2. In a second step we have provided a very detailed documentation regarding the package (Report #1), including all relevant information with regard to the Liechtenstein pension system. (This documentation is also available through the R-package as vignette("model")).

3. Next, we have determined a set of plausibility checks regarding all relevant input parameters for all the functions in the package. Based on these checks we could already draw some preliminary conclusions regarding the dependency of the optimal solution on specific input parameters. This also helped us significantly in reducing undesired outcomes (such as ‘Moral Hazard’ implying that a person finances his pension benefits by heavily borrowing from the bank without the intention of ever paying back his loan).

4. Based on these checks and the literature we have compiled a final grid of plausible parameters to use as an input for our large-scale optimization approach. Due to the large number of possible combinations we had to be very sparse regarding such combinations. Of the resulting parameter grid, we eliminated some additional (infeasible) combinations ending up with a final set of 3’110’400 feasible parameter combinations.

5. Due to the very time-consuming full-parameter optimization (approx. 25 minutes on a standard CPU), we have decided to only optimize 5 parameters:

   • c consumption share of remaining income after contribution to pillars one and two
   • alpha amount of retained wealth per year when managing assets in retirement as “self-man-aged pension”
   • w optimal asset allocation in stocks, bonds and real estate for third pillar savings Each of these optimizations takes about 10 minutes. To jump-start our results we have heavily invested (using the none-FFF-budget of the Chair in Finance) in some large-scale optimization clusters on Amazon AWS, where we parallelized our calculations across three clusters holding 96 CPU-cores each. After finishing approx. 500’000 of the necessary optimizations we had to terminate the approach due to its considerable cost and are currently running the remaining optimizations on our own cluster with 40 CPUs, managing about 6’000-10’000 calculations a day. Based on these numbers and the availability of our cluster we expect to finish the calculation at the end of 2021.

6. Based on our results so far, we have run one- and two-dimensional comparative static analyses on the dependent variables regarding variations in the independent variables and were able to determine the most relevant drivers of the pension decisions. We regard these results as valid in terms of their general direction, but will postpone a more detailed analysis until we have more optimizations available.

7. We have made heavy use of Machine Learning techniques (implemented in Python) to train our heuristical model for a near-optimal and fast approximation of optimal pension decisions for the individuals insured in the Liechtenstein pension system. Among the three trained models (linear regression, K-nearest neighbors and a random forest with tuned hyperparameters) we find surprisingly good out-of-sample performance especially in case of the tuned random forest.

8. Last, we have developed an online app using the software package shiny (available at https://apps.resqfin.com/pfli) that makes our results publicly available. In this app, anyone can set up his/her initial situation and use our heuristics to retrieve near-optimal solutions for his/her specific situation. However, due to the sparse availability (we live-report percentages covered in the app) of optimizations esp. in some areas of the parameter grid, we would refrain from relying on these results yet. However, the underlying model self-updates regularly and results improve continuously.